收藏級(jí)干貨 | 充分搞懂高斯光束：從光束質(zhì)量到透鏡選型的全鏈路解析

導(dǎo)語(yǔ)

在激光光學(xué)系統(tǒng)的設(shè)計(jì)中，我們常常會(huì)遇到一個(gè)令人頭疼的現(xiàn)象：

明明按照幾何光學(xué)公式1/f = 1/s + 1/s’計(jì)算好了透鏡位置，為什么實(shí)際測(cè)量到的光斑大小和位置總是有偏差？為什么想把光斑聚焦得更小，卻發(fā)現(xiàn)焦深變得極短？

答案在于：激光不是直線(xiàn)，而是波。

大多數(shù)激光應(yīng)用都假設(shè)光束是理想的高斯光束（Gaussian Beam）。它的傳播規(guī)律、聚焦特性與我們熟悉的傳統(tǒng)成像光學(xué)大相徑庭。如果繼續(xù)沿用簡(jiǎn)單的幾何光學(xué)思維，你的激光系統(tǒng)設(shè)計(jì)注定會(huì)存在誤差。

今天，我們將基于經(jīng)典教程，深入剖析高斯光束的傳播機(jī)理、薄透鏡公式修正以及“焦距變換"這一反直覺(jué)現(xiàn)象。

?

01 什么是真正的高斯光束？

The Anatomy of a Gaussian Beam

當(dāng)我們談?wù)摷す馐鴷r(shí)，我們首先要明確它的能量分布。理想的基模激光束（TEM00）其輻照度分布是軸對(duì)稱(chēng)的，且隨著離軸距離的增加呈高斯函數(shù)衰減。

但在工程實(shí)踐中，沒(méi)有真正的理想光束。我們通常引入 M2?因子（光束質(zhì)量因子） 來(lái)描述真實(shí)激光束與衍射極限下的理想高斯光束的差距。

一個(gè)理想高斯光束的輻照度分布公式如下：

??

這里有一個(gè)關(guān)鍵概念：光束半徑 w(z）。

它并不是光束的“邊緣"，而是指輻照度下降到峰值 I0的 1/e2（約13.5%）處的徑向距離。

圖1: 高斯光束的束腰定義為輻照度為其較大值1/e2 (13.5%) 的位置

02 束腰、發(fā)散與瑞利長(zhǎng)度

Understanding Propagation Parameters

激光束在空間傳播時(shí)，其直徑并不是恒定的。受衍射效應(yīng)影響，光束會(huì)經(jīng)歷“收斂-束腰-發(fā)散"的過(guò)程。

• 束腰 (Beam Waist, w?)：光束直徑最小的位置。

• 發(fā)散角 (Divergence, θ)：描述光束在遠(yuǎn)場(chǎng)擴(kuò)散程度的參數(shù)。

這兩者之間存在著一個(gè)類(lèi)似于“測(cè)不準(zhǔn)原理"的制約關(guān)系：

? ?

劃重點(diǎn)： 束腰越小，發(fā)散角越大；束腰越大，光束準(zhǔn)直性越好。這就是為什么激光擴(kuò)束鏡通過(guò)放大光束直徑，反而能獲得更準(zhǔn)直光束的物理原因。

此外，還有一個(gè)工程師必須掌握的參數(shù)——瑞利長(zhǎng)度 (zR)。

它定義了光束橫截面積增加到束腰處兩倍（即直徑增加到 √2 w?）時(shí)的軸向距離。

? ?

瑞利長(zhǎng)度決定了激光加工中的焦深（Depth of Focus）。如果你需要切割厚材料，你不僅需要極小的光斑，還需要足夠長(zhǎng)的瑞利長(zhǎng)度。

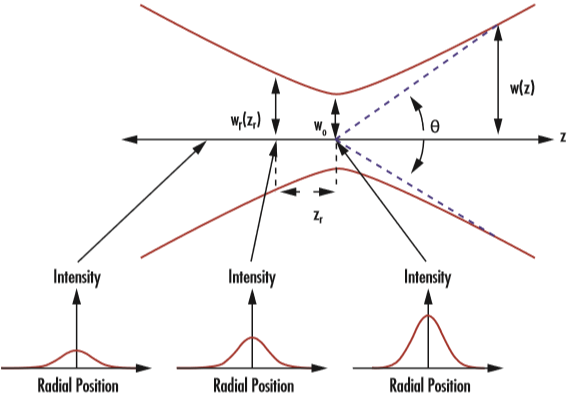
圖2: 高斯光束通過(guò)其束腰 (w0)、瑞利長(zhǎng)度 (zR) 和發(fā)散角 (θ) 定義

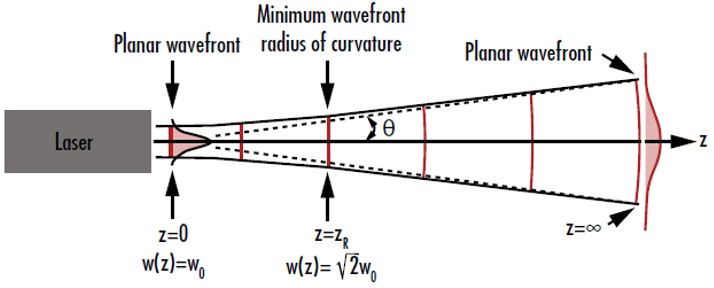
圖3: 當(dāng)高斯光束離束腰非常近和非常遠(yuǎn)時(shí)，其波前曲率接近于零

?

03 修正：高斯光束的薄透鏡公式

The Gaussian Thin Lens Equation

這是最容易“翻車(chē)"的地方。

在傳統(tǒng)成像光學(xué)中，我們使用公式

但在激光光學(xué)中，我們需要引入Sidney Self在1983年推導(dǎo)的高斯薄透鏡公式：

? ?

• s：輸入束腰到透鏡的距離

• s’：透鏡到輸出束腰的距離

• f：透鏡焦距

注意： 當(dāng)瑞利長(zhǎng)度zR趨近于0時(shí)，這個(gè)公式才退化為我們熟悉的幾何光學(xué)公式。對(duì)于長(zhǎng)焦距透鏡或大光斑系統(tǒng)，直接套用幾何公式會(huì)導(dǎo)致焦平面位置計(jì)算嚴(yán)重偏差。

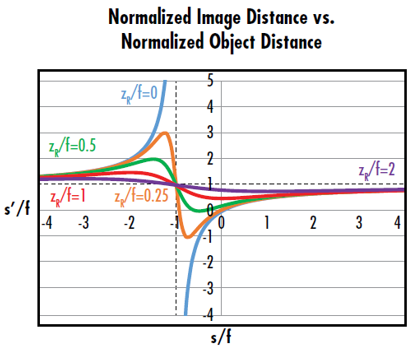
圖4: zR/f=0 的曲線(xiàn)對(duì)應(yīng)于傳統(tǒng)的薄透鏡公式。zR/f>0 的曲線(xiàn)表 明，高斯成像具有瑞利長(zhǎng)度所定義的最小和較大成像距離

為了簡(jiǎn)化計(jì)算，我們通常引入放大倍率 α：

? ?

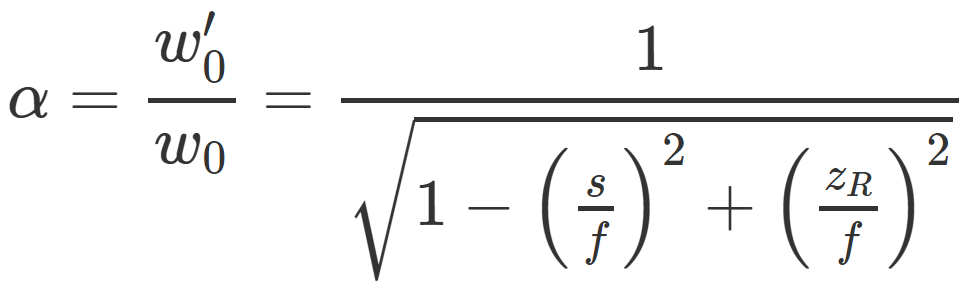掌握了這個(gè)倍率，你就可以算出透鏡后的新束腰大小w?'和新瑞利長(zhǎng)度zR'。

?

04 實(shí)戰(zhàn)：如何獲得最小的聚焦光斑？

Focusing a Laser Beam to a Spot

在激光打標(biāo)、切割或手術(shù)應(yīng)用中，我們的核心目標(biāo)通常只有一個(gè)：把能量集中在盡可能小的點(diǎn)上。

根據(jù)推導(dǎo)，輸出束腰w?'的計(jì)算公式為：

? ?

如何讓 w?'最小？觀(guān)察公式分母，我們需要較大化分母。這意味著：

1.減小焦距f：使用短焦透鏡。

2.增大輸入光束直徑：在聚焦透鏡前加裝擴(kuò)束鏡。

這里有兩種極限情況的簡(jiǎn)化算法，非常適合工程估算：

情況 A：透鏡在瑞利范圍內(nèi) (s ? zR)此時(shí)，輸出束腰簡(jiǎn)化為：

?

這再次印證了：輸入光斑 w?越大，聚焦光斑w?'越小。

情況 B：透鏡遠(yuǎn)離瑞利范圍 (s ? zR)此時(shí)，輸出束腰簡(jiǎn)化為：

??

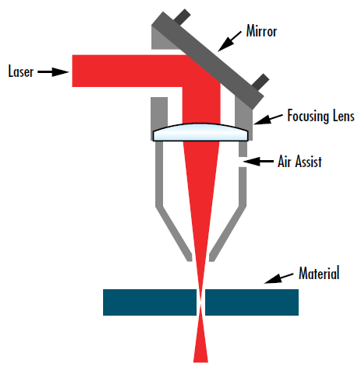
圖5: 將激光束聚焦到盡可能小的尺寸對(duì)于包括這種激光切割裝置在內(nèi)的廣泛應(yīng)用至關(guān)重要

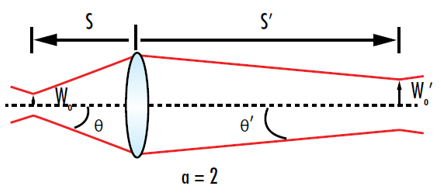
圖6: 對(duì)于放大倍率2，輸出束腰將是輸入束腰的兩倍，輸出發(fā)散將是輸入光束發(fā)散的一半

?

05 反直覺(jué)現(xiàn)象：高斯焦距變換

Gaussian Focal Shift

這是一個(gè)經(jīng)常困擾新手的問(wèn)題：光強(qiáng)較大的點(diǎn)，真的在透鏡的幾何焦點(diǎn)上嗎？

答案是：不一定。

這種現(xiàn)象被稱(chēng)為高斯焦距變換（Gaussian Focal Shift）。

當(dāng)我們將高斯光束聚焦時(shí)，光束半徑最小的位置（即實(shí)際束腰位置）通常會(huì)稍微偏向透鏡一側(cè)，而不是落在幾何焦距f處。

雖然在大多數(shù)高頻應(yīng)用中這個(gè)偏移量很小，但在精密測(cè)量或微納加工中，這個(gè)微小的Δz足以影響加工質(zhì)量。

?最/大光強(qiáng)位置≠幾何焦點(diǎn)?

?只有當(dāng)輸入光束近似為準(zhǔn)直光（s趨向于無(wú)窮大）或聚焦在束腰附近時(shí)，最小光斑位置才會(huì)與幾何焦點(diǎn)重合。

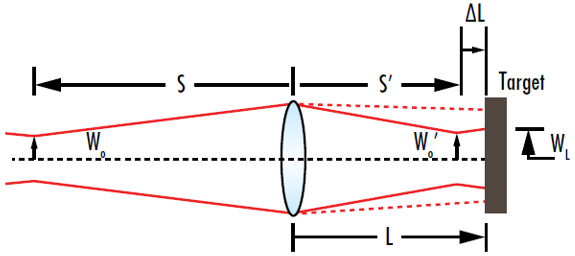
圖7: 目標(biāo)處的光束半徑在聚焦光束的束腰出現(xiàn)在目標(biāo)前的特定位置，而不是目標(biāo)處時(shí)達(dá)到最小值

?

結(jié)尾

高斯光束的傳播并非玄學(xué)，而是遵循著嚴(yán)謹(jǐn)?shù)奈锢砼c數(shù)+學(xué)規(guī)律。

從 M2因子的評(píng)估，到薄透鏡公式的修正，再到對(duì)焦距變換的理解，每一個(gè)細(xì)節(jié)都決定了激光系統(tǒng)的最終性能。在設(shè)計(jì)光學(xué)系統(tǒng)時(shí)，切記不能簡(jiǎn)單地將激光等同于幾何光線(xiàn)。

總結(jié)一下今天的關(guān)鍵點(diǎn)：

1.激光束腰與發(fā)散角成反比。

2.計(jì)算激光聚焦位置時(shí)，請(qǐng)使用高斯薄透鏡公式，而非幾何光學(xué)公式。

3.想要更小的聚焦光斑？請(qǐng)縮短焦距或擴(kuò)大入射光束。

4.警惕“焦距變換"，實(shí)際焦點(diǎn)可能比你計(jì)算的更靠近透鏡。